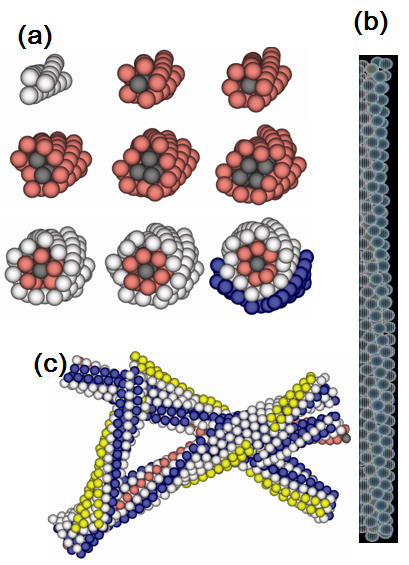
 A simple
A simple
computational model demonstrates the assembly of self-limited filamentous
bundles. The images are taken from dynamic Monte Carlo simulations in which "chiral"
subunits ( with a preference to form twisted arrays of one "handedness")
spontaneously assemble under different interaction strengths and degrees of chirality.
(a) Moderate interactions and moderate chirality
reproducibly lead to bundles of complex internal structure, with
self-limited
diameters, whose size depends on the degree of chirality. Weaker
chirality
allows larger bundles. (b) Lengthwise view of a self-limited two-layer
bundle. (c) With strong interactions, frustration is relieved by
defects,
which enable the formation of branched networks and irregular bundles.
The
assembly of filamentous bundles with controlled diameters is essential for
structure and regulation in biological systems and desirable for the
development of nanomaterials. The objective of
this project is to determine, without assumptions about assembly pathways or
assemblage geometries, if chirality can result in stable bundles with finite diameters. To
answer this general question, the MRSEC investigators constructed a minimal
model for pairwise chiral interactions that
drive assembly into filamentous bundles. They then combined free energy
calculations and recently developed path sampling techniques explore the
structures that spontaneously assemble for varying degrees of chirality. The simulations
have demonstrated that frustration due to chirality can result in regular self-limited bundles for a range
of interaction strengths. With stronger
interactions, however, the frustration is relieved by defects, which give rise
to branched networks or irregular bundles. While some regular self-limited
structures that emerge from model trajectories can be modeled as twisted
filaments arranged with local hexagonal symmetry (as done in several prior
equilibrium calculations), other structures are surprising in their complexity
and could not have been predicted with geometrical equilibrium arguments.