Background: A bar magnet has two poles, denoted as +1 and -1 magnetic charges. Patterned structures
consist of many magnets (Fig. 1), where the square array (Fig. 1a) does not, whereas the honeycomb
(Fig. 1b) has, net magnetic charges (or magnetic monopoles). Under a magnetic field these local
magnetic monopoles will move (Fig. 1c). This latter structure is called “spin ice”, because it has
a large number of nearly degenerate configurations.
This work: We propose a theoretical model of the dynamics in artificial spin ice under an applied
magnetic field, where magnetization reversal (Fig. 2) is mediated by domain walls carrying two units of
magnetic charges, in agreement with experiment.
(Shen is a JHU undergraduate)
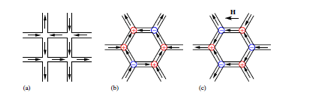
Fig.1: (a) A configuration of square spin ice with no
magnetic charge,(b) honeycomb spin ice has magnetic
Charges, (c) magnetized honeycomb spin ice.
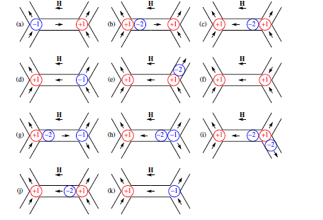Fig. 2: Magnetization reversal in honeycomb spin ice.
(a)-(d) A domain wall (DW) is emitted at one end and
absorbed at the other end, and absorbed at the junction.
(e)-(f) a new DW can be emitted by a large H field,
(g)-(k) a DW encounters a magnetic charge and emits a DW.
