The discovery of superconductivity in twisted graphene systems has generated tremendous interest, where low-energy flat bands with strong correlations play a key role. Flat bands may also be induced by moiré patterning in the transition metal dichalcogenides (TMDs), however experimental observation of superconductivity has remained absent. This raises the question as to whether superconductivity is a universal feature in flat-band, two-dimensional systems or there is some unique graphene-specific feature that makes superconductivity favorable.

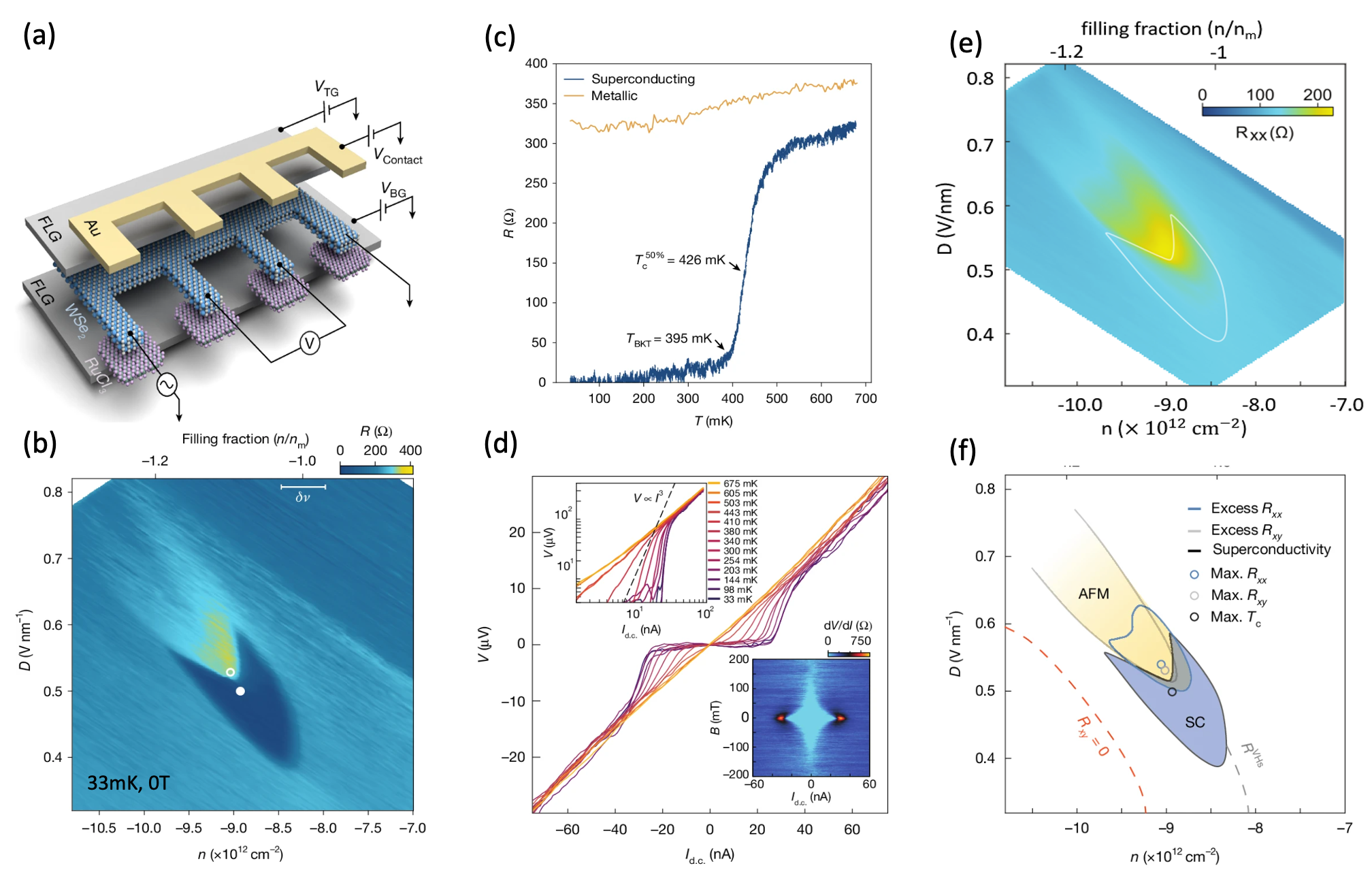
Here we report superconductivity (SC) in 5.0° twisted bilayer WSe₂, appearing in a limited region of displacement field and density adjacent to a metallic state. Theoretical calculation shows that the metallic state arises from aFermi surface reconstruction due to antiferromagnetic (AFM) order. Analysis of the SC–AFM phase diagram suggests that the SC may have exotic order, stabilized by spin fluctuations.

Our results establish that moiré superconductivity extends beyond graphene structures. This has important implications on the theoretical models of superconductivity in 2D flat bands on general grounds,  since it should now accommodate substantially different materials systems. Moreover, material properties that are absent in graphene but intrinsic among the TMDs such as a native band gap, large spin-orbit coupling, spin-valley locking and magnetism offer the possibility to access a broader superconducting parameter space than graphene-only structures.